本文共 1423 字，大约阅读时间需要 4 分钟。

最短路径问题—Dijkstra算法

Dijkstra算法：

简称dij(弗洛伊德)算法

用来计算从一个点到其他所有点的最短路径的算法，是一种单源最短路径算法。也就是说，只能计算起点只有一个的情况。

优点：时间复杂度是 O (N2)，比Floyd快

缺点：它 不能处理存在负边权的情况

算法思路

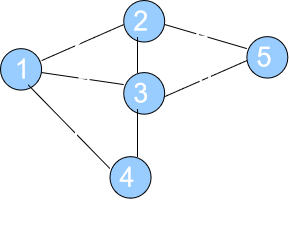
从起点到一个点的最短路径一定会经过至少一个“中转点”（例如下图1到5的最短路径，中转点是2。特殊地，我们认为起点1也是一个“中转点”）
显而易见，如果我们想求出起点到一个点的最短路径，那我们必然要先求出中转点的最短路径
（例如我们必须先求出点2 的最短路径后，才能求出从起点到5的最短路径）。

我们把点分为两类，一类是已确定最短路径的点，称为“白点”，另一类是未确定最短路径的点，称为“蓝点”。
如果我们要求出一个点的最短路径，就是把这个点由蓝点变为白点。从起点到蓝点的最短路径上的中转点在这个时刻只能是白----点。
Dijkstra的算法思想，就是一开始将起点到起点的距离标记为0，而后进行n次循环，每次找出一个到起点距离dis[u]最短的点u，
将它从蓝点变为白点。随后枚举所有的蓝点vi，如果以此白点为中转到达蓝点vi的路径dis[u]+w[u][vi]更短的话，
将它作为vi的“更短路径”dis[vi]（此时还不确定是不是vi的最短路径）。
1 2
3 4

接下来的两轮循环将4、5也变成白点。N轮循环结束后，所有的点的最短路径即能求出。

代码

#include<iostream>#include<algorithm>#include<cstdio>#include<cstring>#include<cmath>using namespace std;int x[110],y[110],n,m,s,t,l,r,u,g;bool b[110];double a[110][110],mn[110];void in(){   	cin>>n;	for(int i=1;i<=n;i++)	{   		cin>>x[i]>>y[i];	}cin>>m;	memset(mn,0x7f7f7f7f,sizeof(mn));	for(int i=1;i<=m;i++)	{   		cin>>l>>r;		a[l][r]=sqrt(abs(x[l]-x[r])*abs(x[l]-x[r])+abs(y[l]-y[r])*abs(y[l]-y[r]));		a[r][l]=sqrt(abs(x[l]-x[r])*abs(x[l]-x[r])+abs(y[l]-y[r])*abs(y[l]-y[r]));	}cin>>s>>t;}void Dijkstra(){   	mn[s]=0;	for(int i=1;i<=n;i++){   		g=0x7f7f7f7f;		for(int j=1;j<=n;j++){   			if(!b[j]&&g>mn[j]){   				u=j;g=mn[j];			}		}b[u]=1;		for(int j=1;j<=n;j++){   			if(!b[j]&&a[u][j]){   				mn[j]=min(mn[j],mn[u]+a[u][j]);			}		}	}}int main(){   	in();	Dijkstra();	printf("%0.02lf",mn[t]);}

转载地址：http://zgcr.baihongyu.com/